Summary:

There is debate amongst coaches and researchers as to whether we can actually “predict” injuries. There are two main hurdles that must be considered when attempting to use injury prediction models in practice. This article discusses assumptions regarding injury base rates and whether more accurate prediction models actually yield better decision-making processes. Practical recommendations are then made for coaches based on these statistical assumptions for current and future practice.

Note to reader, all internal references are hyperlinked to the source material

Coaches and researchers debate whether we can actually “predict” injuries. This debate is complicated by the many companies that advertise that they use sophisticated algorithms to build injury-prediction profiles of athletes to guide future training. Despite years of research discussing the utility of predicting Anterior Cruciate Ligament (ACL) injuries from movement assessments (e.g., see Bahr, 2016; Hewett, 2016; Nilstad et al., 2021; Russo et al., 2021), there are several reasons that practitioners may still be interested in using pre-existing, or perhaps even building their own, injury prediction models. A main reason is to justify training interventions that aim to mitigate the injury before it occurs. Additionally, and at risk of sounding a bit insensitive, injury prediction models can be relevant for (sport) organizations attempting to manage their labour assets (i.e., their workers/players) by forecasting costs associated with injuries before they occur. A salient injury that coaches might want to predict is ACL tears, given their relatively high prevalence, cost (which can exceed USD 277 billion annually (Yelin, 2003)), and time required for rehabilitation.

Previously, researchers and practitioners made relatively simple linear or logistic regression models to predict injuries. For example, Hewett et al. (2005) monitored knee valgus motion and moments during a vertical drop jump to assess the risk of ACL injury in adolescent athletes. In their study, they built a logistic regression model (which outputs either a “yes” or “no”) that predicted whether an individual sustained an ACL injury. Since this seminal work, the same group identified other variables associated with ACL injuries. For example, Myer et al. (2010) reported associations between ACL injuries and tibia length, knee flexion range of motion, body mass, and quadriceps-hamstring ratio. As technology advances, it becomes easier to conveniently collect more diverse data (e.g., biomechanical data, social determinants of health, psychological status). Therefore, researchers and practitioners may start to leverage machine learning algorithms to improve the accuracy of prediction models by integrating these variables in nonlinear ways (see Van Eetvelde et al., 2021 for a relatively recent review).

---

George Box stated that “all models are wrong, but some are useful.” Therefore, the question remains as to how useful these injury prediction models are for improving practical decision-making and intervention design. There are two major hurdles not often mentioned when discussing the potential utility of prediction models. I do not intend to suggest whether someone should (not) use injury prediction models, but instead share some technical concerns that I firmly believe researchers and practitioners must consider. Knowledge of these technical concerns can help shape professional practice.

There are two points that researchers and practitioners must consider when interpreting the outputs of these models; 1) the base rate of injuries and 2) the assumption that better predictions will result in better decision, minimizing the use of interventions (and, perhaps, may result in worse decisions).  After outlining these points below, I will share my thoughts on how to best move forward with assessing movement to guide intervention design.

The base rate of injuries must be considered

The problem

First, we need to discuss the sensitivity and specificity of a model. Sensitivity refers to the model’s ability to correctly identify the construct of interest (i.e., ACL injury). In contrast, specificity refers to the model’s ability to discriminate against those who would not have the construct of interest (i.e., those without ACL injury). The figure below depicts both constructs:

Now, let’s move on to a more salient example and use Hewett et al.’s (2005) logistic regression model to assess ACL tear risk based on knee abduction loads during a vertical drop jump. Their model reported a sensitivity of 78% and a specificity of 73%. This means that their model correctly identified 78% of all ACL injuries and correctly ruled out 73% of all non-injury cases.

The performance of this model looks promising, at least initially. The problem is that interpreting the sensitivity and specificity alone is misleading without considering the baseline prevalence of ACL injuries. Omitting this information in our interpretations is referred to as the base rate fallacy, which psychologists have studied for decades (e.g., Kahneman and Tversky, 1973, Bar-Hillel, 1980).

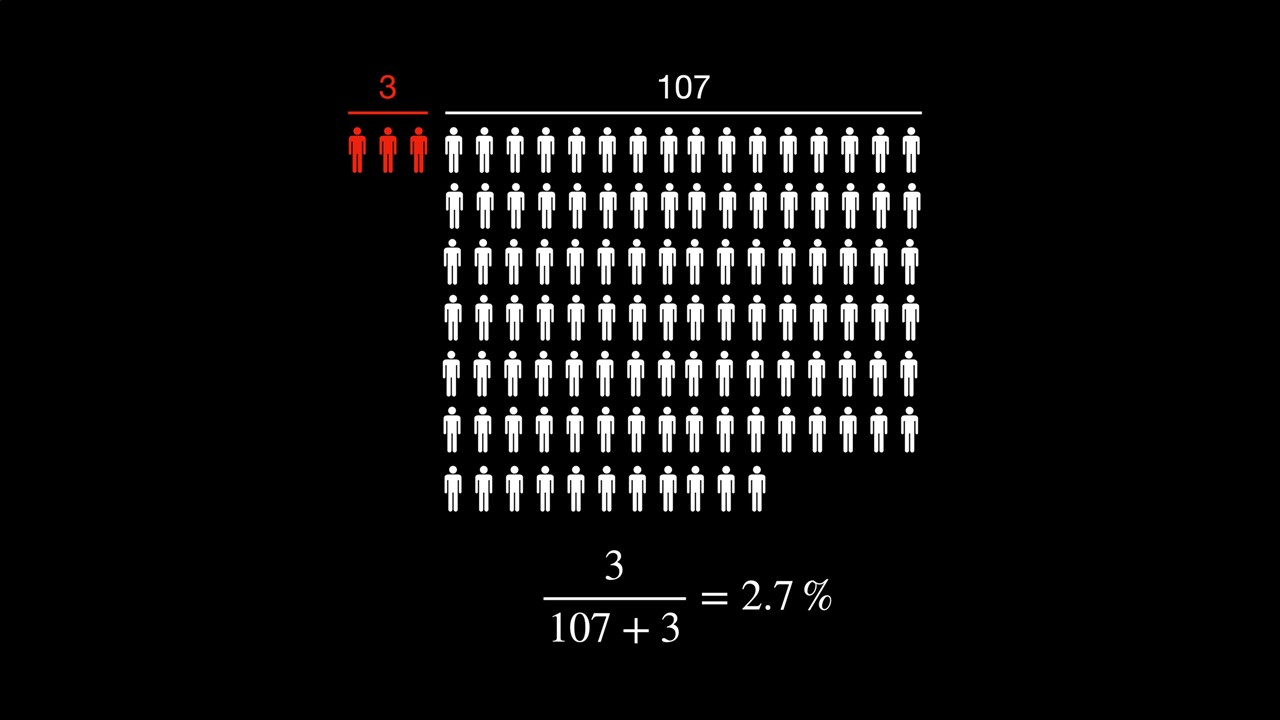
Building on this example we can illustrate the implications of not considering the base rate when interpreting the sensitivity and specificity of a model. Consider that the prevalence of ACL injuries per season is about 1.1% for adolescent female soccer players (Gornitzky et al., 2016). In other words, without any extra information, we should expect that an adolescent female soccer athlete has a 1.1% risk of tearing their ACL this season. Next, let’s assume we have assessed 400 athletes with this logistic regression model. Visually, the figure below highlights what we would expect based on the (sensitivity and specificity) characteristics of Hewett et al.’s (2005) logistic regression model highlighted in the previous paragraphs:

After considering the base rate, the person’s actual risk of tearing their ACL, given that the model predicts an ACL tear, is the ratio of true positives to total positives (see below):

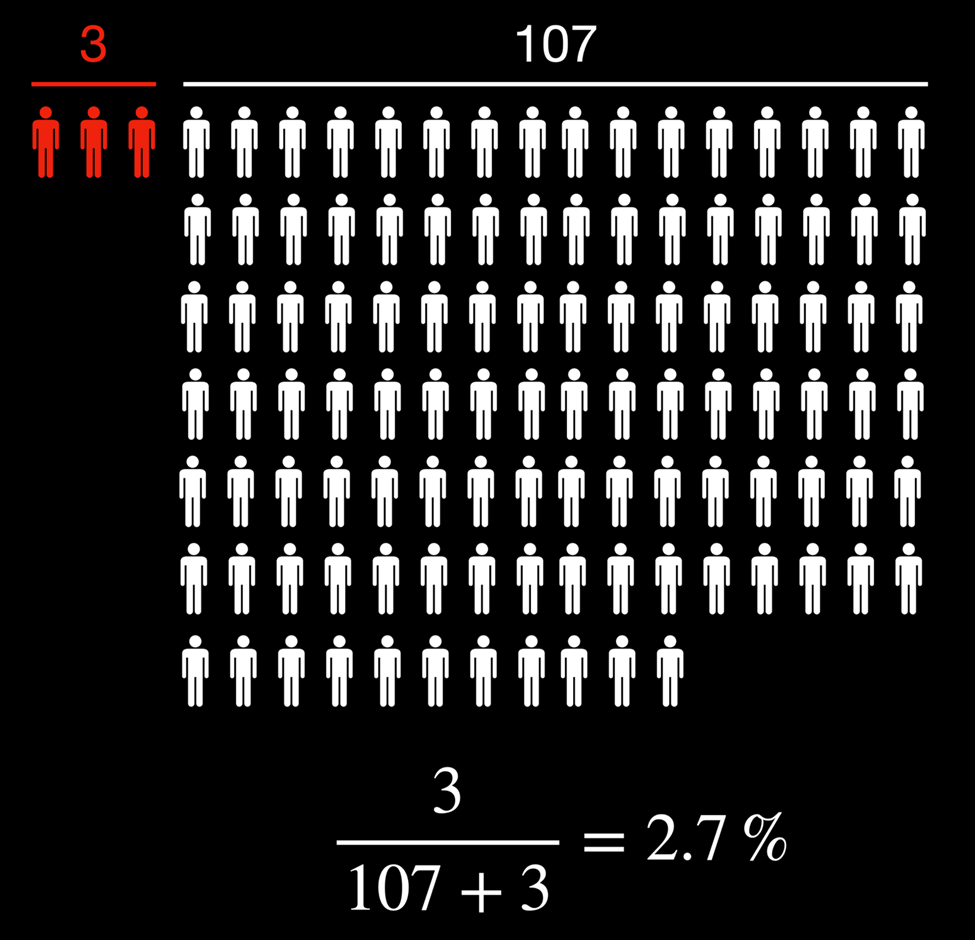
Given that the model predicted an ACL tear, the updated 2.7% probability of the athlete tearing their ACL isn’t overly convincing relative to the baseline of 1.1%. Perhaps this is because we’ve used a simple logistic regression where the only independent variable was knee abduction moments during a vertical drop jump. Surely the updated probability will be much higher if we use a larger battery of tasks, more variables, and more sophisticated models, right?

Unfortunately, not quite. Even if we had a state-of-the-art machine learning model with 100% sensitivity and 99% specificity, the updated probability of these adolescent female athletes tearing their ACL, given the model predicts they would get injured, is now 50% (you can verify the calculations using this diagnostic test calculator). This model performance is much better than the logistic regression from before and probably unreasonable to attain in practice. However, the probability that an athlete will get injured, given that the model predicts an ACL injury, is still only about the same as flipping a fair coin.

---

Potential solutions

Several authors have recently written about a complex systems approach to predicting injuries. For example, Bittencourt et al. (2016) wrote an excellent paper outlining that a complex systems approach for sports injuries may be more fruitful than simple risk factor identification. Briefly, this complex systems approach accounts for the interconnectedness between variables and multiple levels of the biological system by seeking patterns of interactions between determinants to understand why and when injuries may emerge. The Rebel Movement Blog also wrote a fantastic article inspired by a recent paper by Stern et al. (2020) describing athletes as “hurricanes” who constantly evolve and adapt based on their interaction with the environment. One of the main arguments by Stern et al. (2020) is that:

“as with the tracking of a volatile weather pattern like a hurricane, frequent sampling of variables through athlete testing is a prerequisite to understanding the behavior of the human system and to detecting when there is a change in the resistance of the system to injury.”

Therefore, not only should a dynamical systems-based approach to prediction models be taken, but researchers and practitioners should make more frequent observations when forecasting injuries. The dynamical systems approach to predicting injuries requires much more research as there are still various gaps in our knowledge of motor control. Albeit, the same simple statistics in the previous section can outline the power of sampling these variables more frequently.

Suppose we still used Hewett’s model with a 78% sensitivity and 73% specificity. As we have already calculated, the probability of an ACL tear, assuming a base rate of 1.1%, is updated to 2.7% if the model predicts an injury. However, what if we were to do more frequent testing of this athlete (either with more testing sessions, more exercise tasks, or a combination of both) and the model kept predicting an ACL injury? What does this do to our confidence in the athlete sustaining an ACL injury?

Table 1. Probability of athlete sustaining an ACL injury based on repeated movement assessments. Each test number would correspond to a hypothetical observation, and the updated probability of test n-1 is used as the prior probability on test n.

Test Number	Prior Probability of ACL Injury (%)	Updated Probability of ACL Injury (%)
1	1.1	2.7
2	2.7	7.1
3	7.1	18.0
4	18.0	38.6
5	38.6	64.5
6	64.5	84.1

---

As we can see from the table above, more frequent testing dramatically improves our confidence that an athlete may sustain an injury. It is important to note that I’m making various statistical assumptions in these calculations and it’s not this clean in practice. Regardless, it still outlines the basic general principles that consistent testing is imperative for practitioners trying to predict injury when designing future training programs.

Less commonly discussed is what this frequent testing would look like in practice. In my opinion, the best way to implement these principles in practice is to make every workout an assessment. Our lab group at the University of Toronto is planning to explore this general concept further by designing and studying various “benchmark workouts” that can prepare people for the demands of their sport while simultaneously functioning as an assessment tool. Stay tuned on this!

The assumption that better predictions result in better decisions and interventions is unjustified

The problem

Before diving into this section, I want to clarify that this section mainly consists of ideas adapted from Wouter van Amsterdam’s blog post titled When good predictions lead to bad decisions. Wouter does an excellent job outlining the math and general theory, so in this section, I am only going to apply it to our previous ACL example.

The general problem with this assumption that more accurate predictions result in better decisions and interventions can be highlighted with a simple example. Suppose Model 1 uses an athlete’s tibia length, knee valgus motion, knee flexion range of motion, and body mass (variables outlined in Myer et al., 2010) to predict ACL injury from a vertical drop jump. Next, suppose the model predicts that the athlete will tear their ACL. In that case, we will implement the ACL-specific program, Intervention A, which might include balance training, emphasis on grooving landing patterns, and prioritizing drills that emphasize perception-action coupling (e.g., Voskanian, 2013). Conversely, suppose the model predicts that the athlete will not get injured. In that case, we will instead implement a general strength training program, Intervention B, including squats, deadlifts, hip thrusts, and other lower extremity “strength” exercises.

Suppose we use Model 1 in practice with our athlete and it predicts “no injury,” so we select Intervention B. However, after some time and more research we discovered that including the quadricep-hamstring strength ratio as an additional factor in a new model, Model 2, improves its accuracy. After assessing the athlete’s quadricep-hamstring ratio, the updated (and more accurate) Model 2 predicts that this person will sustain an ACL injury. Have we made a better decision to switch to Intervention A now that a more accurate model has predicted an ACL tear?

Arguably, this could be a worse decision since the general strength training program (Intervention B) might be more appropriate for addressing the specific quadriceps to hamstring ratio weakness that caused Model 2 to “change” its decision relative to Model 1. Therefore, blindly following the results of the more accurate prediction model has guided the practitioner into making a potentially worse decision regarding which intervention to implement.

Yes, this is a somewhat crude example. However, it highlights the central idea that increased prediction accuracy can lead to poorer intervention decisions because we’re getting a better answer to the wrong question. Rather than understanding the determinants of injury and addressing those specifically, prediction models only attempt to explain the most variance in the data possible. In other words, we are making the classic mistake of conflating correlation with causation. Although this issue might not matter for teams or businesses simply trying to project the costs of injuries to obtain an economic advantage, it does matter for practitioners attempting to select and justify interventions based on these model outputs.

---

Potential solutions

The solution to this second concern is similar to that of the first, whereby a complex systems approach to identifying causality will be critical when building these models. Although the predictions themselves can guide future research, researchers must conduct actual experiments to explore and verify injuries’ complex underpinnings. Bahr (2016) outlined a three-step process to develop and validate injury assessments that can be adapted and embedded in a complex systems approach:

1. Conduct a prospective cohort study to identify risk factor(s) and define cut-off values (i.e., establish an association with a “training” dataset)
2. Validate these risk factors and cut-off values in multiple cohorts (i.e., confirm the model accuracy using a “testing” dataset)
3. Conduct a randomized control trial to test the effect of the intervention program on assessment scores/model outputs and injuries (i.e., establish causation)

Furthermore, researchers and practitioners will need to move beyond single biomechanical variables in these models/assessments. For example, the literature has clearly established that it is unlikely that monitoring frontal plane knee motion alone during a single movement assessment can prospectively discriminate between those who do and do not sustain an ACL injury (e.g., Krosshaug et al., 2016; Romero-Franco et al., 2020; Petushek et al., 2021; Nilstad et al., 2021). Yet, researchers consistently find large displacements and velocities in frontal and transverse plane knee motion, as well as minimal sagittal plane knee motion, when people tear their ACLs in team sport settings (e.g., Olsen et al., 2004; Krosshaug et al., 2007; Shimokochi et al., 2008; Hewett et al., 2009; Koga et al., 2010; Carlson et al., 2016; Lucarno et al., 2021). Therefore, it is more likely that the general knee movement behaviours in all three planes (Quatman et al., 2010) across multiple task, environmental, and personal constraints (Davids et al., 2003) is what coaches should assess, not the behaviours of any single task and constraint combination at a single instance in time. This methodology is summarized nicely in Frost et al.’s 2015 research. They demonstrate that a battery of lower extremity exercises performed with various loads and velocities predict the frontal plane knee motions adopted in fireground-specific tasks, such as sledgehammer chops, a forced-entry task, firehose drags, firehose pulls, and a heavy sled drag. However, no single task alone was predictive of the movement behaviours that emerged in these fireground-specific tasks.

---

In addition to a more encompassing biomechanical assessment, a more holistic view of risk factor identification and establishing causation is essential for justifying future interventions. For example, more emphasis needs to be placed on other social (e.g., Truong et al., 2020) and psychological (e.g., Adern et al., 2016; Chan et al., 2017) factors that contribute to these injuries. Considering these factors requires us to build a more holistic web of determinants to identify the emerging injury patterns (e.g., Bittencourt et al., 2016). It is only by understanding why the injury emerges, which can only be done with a transdisciplinary approach, that practitioners can work backwards to design an intervention that targets critical nodes in the complex web of determinants.

Summary

The low base rate and the unjustified assumption that more accurate prediction models result in better practical decisions are two challenges with the current injury prediction model paradigm. In addition to additional research uncovering the complex web of determinants, adopting a systems-based approach with more frequent assessments of a more comprehensive array of variables (beyond just biomechanical) is crucial for coaches to improve their assessment design, intervention design and practical decision-making. These factors are especially important for coaches to consider when deciding whether to purchase sophisticated equipment with flashy marketing that offers lofty promises, when leveraging existing models in the literature, or building their own prediction models in professional settings.

Biography

Steven Hirsch is currently a Ph.D. candidate at the University of Toronto studying biomechanics and motor control. His main professional interests include improving athletic performance, reducing injury risk, acquiring motor skills safely and effectively, and developing statistical tools and technologies that allow researchers, practitioners, and individuals to realize these objectives. Steven is also extremely interested in the general process of using statistical tools and Implementation Science to translate data and scientific principles into action for performance, health, and wellness initiatives